We’ve all grown up with the real number system—it’s so deeply ingrained in how we think about math that it can be hard to imagine an entirely different world of numbers. But that’s exactly what p-adic numbers offer: a complete reversal of the rules we’re used to.This time, I will do my best to perform this seemingly insurmountable task of explaining this extremely niche and puzzling branch of number theory in a tiny article, and finally share my long-held infatuation with this topic with all of you. So, freshen up those neurons, set your math fears aside, and let us jump right into it!

Imagine a number that goes to infinity after a decimal point, like 0.9999999…, fairly straightforward right?  Now, flip it so that it goes to infinity on the left of the decimal point: …9999999.0. There you have it, that’s a p-adic number! More precisely, a 10-adic number because you’re writing in base 10. Arranging numbers this way introduces a novel idea of what makes numbers be close to each other. Normally, numbers which agree to the right of the decimal point are closer together. This is anything but normal—in p-adic systems, numbers are considered closer if they match on the left side of the decimal point, not the right!

You can now add, subtract, and multiply different 10-adic numbers. Let’s look at an example:

      ...21032121

+    …00000001

---------------------

      ...21032122

For subtraction, you add the negative of one number to another. In p-adics, negatives can be represented without signs. This can be proven by the following:

      ...99999999

+    …00000001

---------------------

      ...00000000

The sum of ..9999999 and one in p-adics is equal to 0. While it might seem like this addition would leave a trailing 1 at the end, that never happens—because the 0s stretch infinitely to the left. You know what else added to 1 is equal to  0? -1.

That’s right, …99999999 is the 10-adic representation of -1. If you’re familiar with data representation in computers, you might be aware of the two’s complement. That same method can be used to find the negative counterpart of a p-adic number.

In the case of 10-adics, you first take the 9’s complement, which is the difference between each individual digit and 9, and then you add 1 to it. Let’s take …25673894.

Adding 1 to …74326105, we get ..74326106.    Adding this to the original, the sum comes out to be zero!

    ...25673894

+  …74326106

---------------------

      ...00000000

All this time, we have only dealt with 10-adic numbers; a base system we’re familiar with, but also a base system which brings forth a lot of problems which are too nuanced to be discussed here. Instead, using a prime number as the base, which gives us true p-adic numbers, makes the system far more useful, mathematically consistent, and free from the complications that arise in base-10.

To write 3 or 5-adic numbers, we need to get familiar with modular arithmetic. It is a way of counting numbers that works like an analogue clock, looping back on itself over and over again. Imagine it’s 9 o’clock now. What time will it be in 5 hours? Not 14 o’clock, we say it’s 2 o’clock, because clocks wrap around after 12:

14 modulo 12 is 2

Coming back to p-adics, 25 can be represented in 3-adics as:

• 
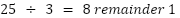
  The units digit (coefficient of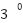 ) is 1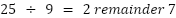
• 

The total remainder up to this point is 7.
We've already used 1 (from step 1), so we subtract that:

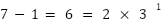
So the 3¹ digit is 2

• 
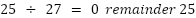
  Now subtract the parts we've already used:
  
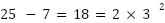
  So the 3² digit is 2

The value of 25 in 3-adics is …00000221

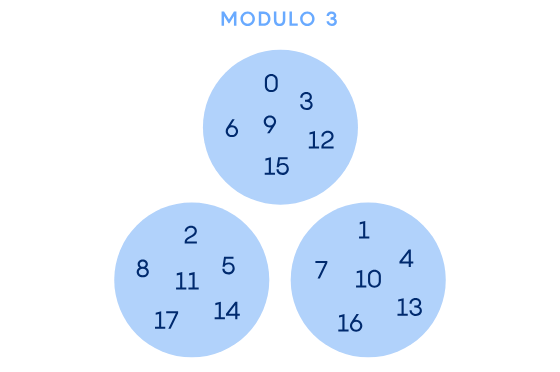
We can get an intuitive sense of how p-adic numbers work by imagining the integers grouped into “rooms” based on their values modulo 3.

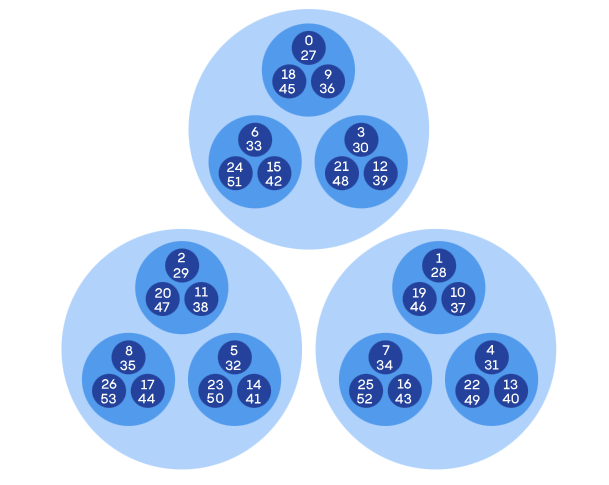
Dividing the integers further using higher powers of 3 creates smaller and smaller “rooms,” stacked on top of each other infinitely, a tower of increasingly precise groupings.

You can see, in this way, how numbers which share rooms or powers of 3 are closer to each other then the ones which don’t. As the image shows, 45 lies closer to 0 than 1 does in the 3-adic system.

What is the use of all this math, you ask? Well, finding rational solutions to advanced polynomial equations is unimaginably tedious without these trusty p-adics. Instead of going through them with the good ol’ real number system which is inundated with irrational solutions, mathematicians opt to first solve them in different p-adic worlds. Moreover, Some branches of theoretical physics and biology also use them to model tree-like hierarchical systems which share the same notion of closeness as p-adics!

P-adics demonstrate how math is neither firm nor rigid, but rather flexible, allowing us to bend its rules to conform to even our questions, let alone answers.

Credits:

- Figure 1: Image from “An Infinite Universe of Number Systems” by K. Houston-Edwards, Quanta Magazine (2020). Used here under fair use for educational purposes.