Carl Friedrich Gauss: The Prince of Mathematics

Carl Friedrich Gauss was a German mathematician regarded as one of the greatest of all time due to his extraordinary contributions. He made major advances in number theory, geometry, probability theory, geodesy, planetary astronomy, the theory of functions, and potential theory, including electromagnetism.
He studied mathematics at the University of Göttingen and soon became the finest mathematician of his era and the leading figure of the German-speaking world. Gauss is often regarded as a successor to Leonhard Euler’s work.
Gauss’s first major mathematical breakthrough occurred in 1792, when he discovered that a regular 17-sided polygon could be constructed using only a compass and straightedge. This finding was significant because it provided insight into the factorization of polynomial equations and helped lay the groundwork for Galois theory.
In 1797, Gauss proved the fundamental theorem of algebra, which states that every polynomial with real or complex coefficients has as many roots as the degree of the polynomial.
He also worked on the Beltrami equation, which plays an important role in mapping curved surfaces such as the Earth.
Gauss made groundbreaking contributions to geometry, particularly differential geometry. He demonstrated that the curvature of a surface can be determined by measuring angles and distances directly on that surface. This insight refined the field of geodesy and later influenced scientific developments such as Einstein’s theory of general relativity.
He also explored Euclid’s parallel postulate, which asserts that parallel lines never meet. His investigations led to the emergence of non-Euclidean geometry, where this postulate does not hold and the geometry of space is curved, as seen in hyperbolic geometry.
This new form of geometry did not invalidate classical mathematics but introduced a different set of rules from Euclidean geometry.
Among Gauss’s other notable contributions are Gaussian quadrature and the Gauss–Seidel method. Gaussian quadrature provides a technique for approximating the area under a curve when exact integration is difficult or impossible.
The Gauss–Seidel method is an iterative technique for solving systems of simultaneous linear equations. Instead of solving all equations at once, it improves the solution step by step. These methods remain essential in modern computer simulations, including applications in electrical circuit analysis.
Gauss also discovered the deep connection between the arithmetic–geometric mean (AGM) and elliptic functions, allowing for more accurate and efficient solutions. His advanced understanding of complex analysis, developed well before formal publication by others, laid the foundation for modern engineering and physics.
He introduced the Jacobi theta functions, which describe recurring patterns found in advanced mathematics and physics, and helped develop identities such as the Jacobi triple product, building on earlier work by Euler.
Gauss also investigated modular transformations and their changing behaviors under different conditions.
In addition, Gauss made foundational contributions to hypergeometric functions, which generalize logarithmic, trigonometric, and exponential functions. He was among the first to rigorously study the convergence of infinite series, a concept that remains vital in probability and statistics today.
Gauss’s work continues to have profound applications across STEM disciplines, including computer science, physics, mathematics, and statistics. In recognition of his immense impact, he earned the title Prince of Mathematics.
This honor is attributed to Johann Peter Gustav Lejeune Dirichlet, one of Gauss’s most prominent students and successors in number theory.
Similar Post You May Like
-
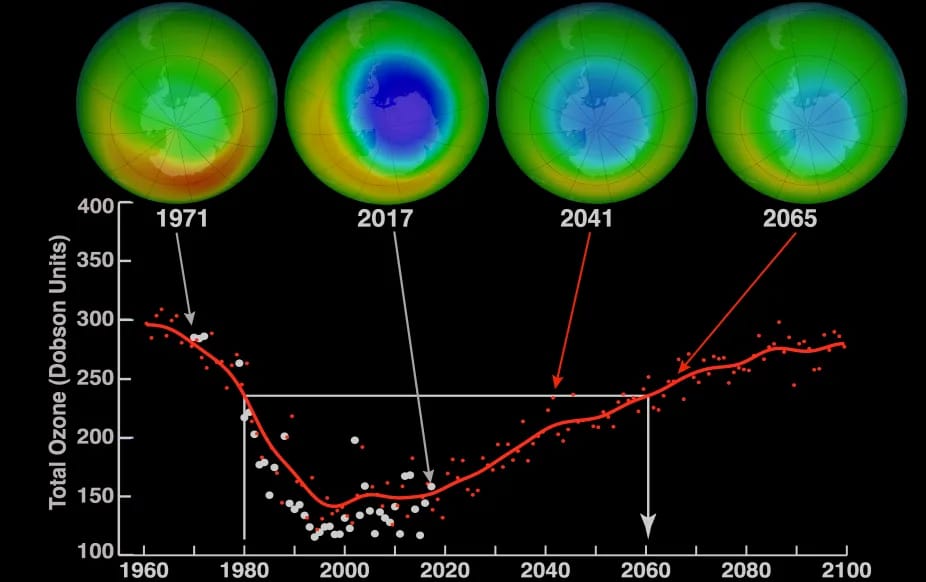
CFCs, HFCs and their long, troubled history
At its peak, the ozone hole covered an area 7 times larger than the size of Europe, around 29.9 million km2, and was rapidly expanding
-

The Origin of Universe: Deciding point where it all began!
Let us unravel and surf through the ideas throughout ages to understand what the universe and its origin itself was to its inhabitants across history.
-

The Artemis Program
Inspired by the Greek goddess of the Moon, twin sister to Apollo, the artimis program was named on 14 May 2019 by Jim Bridenstine.






