The Architect of Modern Mathematics: Euler’s Legacy

Imagine a person who takes the chaos of numbers, shapes, and symbols and unifies them all under one subject. Well, let me introduce you to a mathematician who not only understood mathematics as a subject, but also as a language. Meet Leonhard Euler, a Swiss mathematician and physicist, known for laying the foundation of various fields in modern mathematics.
To begin with, his first major contribution to mathematics was in the branch of complex numbers. He linked trigonometry, exponentials, and complex numbers by the famous Euler’s formula, which is: eix = cos x + i sin x. A special case for this formula is Euler’s identity: eiπ + 1 = 0. Hence, Euler's formula led to the foundation of complex number theory. It also helped in modern-day electrical engineering, quantum mechanics, and control systems.
Euler also solved the Königsberg Bridge Problem, which led to the foundation of Graph Theory — one of the greatest breakthroughs in mathematics, introducing the concept of graphs that we use almost every day. His contribution to Graph Theory also laid the groundwork for network science, which is important for modern technology as it powers social networks, computer algorithms, and much more.
Another really important contribution of Euler was that he invented many mathematical notations that we use in the modern day. Namely, he introduced the symbols: f(x) for functions, π for pi, e for Euler’s constant, and i for the imaginary unit, which is the square root of −1. He also helped define the gamma function, which generalizes factorials. This made mathematics easier to learn and understand. Without these standard notations, working on mathematics would be like trying to decode a programming language.
Euler also helped make advancements in the field of calculus. He expanded on the use of infinitesimals, which are quantities that are infinitely small but not zero. Furthermore, he introduced various formulas to differential equations, such as the chain rule to calculate the rate of change, the Euler–Lagrange equation, which provides a way to solve these problems by converting them into differential equations, and the Euler–Maclaurin formula, which connects sums and integrals, providing a powerful tool for approximating sums and evaluating definite integrals.
Leonhard Euler not only contributed to calculus but also made major contributions in the field of mechanical physics. Through Euler’s equation, he formulated a set of differential equations that describe the rotational motion of a rigid body. Furthermore, he introduced not only the moment of inertia but also identified the principal axis of inertia. Euler developed the fundamental equations that govern the motion of fluids, known as Euler's equations of fluid dynamics. He also clarified the concept of internal pressure, and his work led to the creation of hydraulic systems. Euler was also the one who studied the behavior of elastic bodies, particularly the elastica, and he derived the formula for the critical buckling load of a slender column — the load where a column will buckle or bend under compression.
Additionally, Euler was the one who came up with number theory — the study of integers and arithmetic functions. It includes concepts like prime numbers, congruences, and additive number theory. He built on Fermat’s work and came up with Euler’s theorem: aϕ(n) ≡ 1 (mod n), which was a generalization of Fermat’s little theorem stating that if p is a prime number, then for any integer a, the number ap − a is an integer multiple of p. This not only provided the basis for cryptography but also made understanding of numerical patterns easier.
Lastly, Euler worked with infinite series long before their formal definition existed. He found the exact sum of reciprocals of squares, known as the Basel problem, which he solved brilliantly. This problem had many mathematicians stunned. However, Euler’s work led to modern analysis and the convergence test, and is being used in fields like calculus, signal processing, physics, and engineering.
To conclude, Euler built the mathematical language we have today. His work unified various fields of mathematics, laid the foundation for computer science and engineering, and gave future scientists mathematical tools to be used in the modern day and age. It would not be a stretch to say that he shaped the way we think, solve, and compute universally!
Similar Post You May Like
-
CFCs, HFCs and their long, troubled history
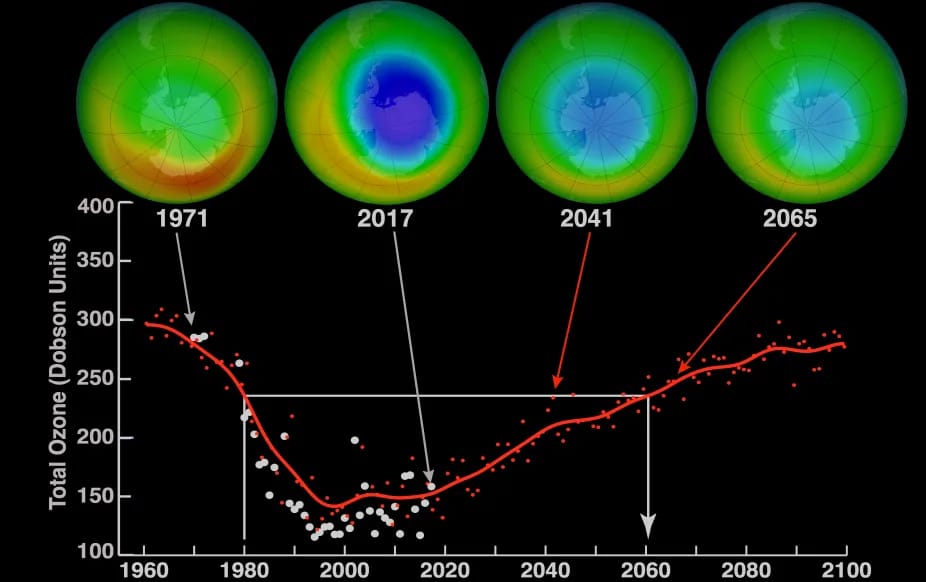
At its peak, the ozone hole covered an area 7 times larger than the size of Europe, around 29.9 million km2, and was rapidly expanding
-

The Origin of Universe: Deciding point where it all began!
Let us unravel and surf through the ideas throughout ages to understand what the universe and its origin itself was to its inhabitants across history.
-

The Artemis Program
Inspired by the Greek goddess of the Moon, twin sister to Apollo, the artimis program was named on 14 May 2019 by Jim Bridenstine.






